线性回归模型假设 #
在数学上对线性回归的定义如下: $$ Y_i = \beta_0 + \beta_1X_i + ϵ $$ 其中\( ϵ \) 表示随机扰动项,是一个无穷小量。
通常有下面的几个假设,
- 误差项零均值:E(ϵ) = 0,
- 同方差性:
$$ Var(ϵ∣X)=σ^2Var(ϵ∣X)=σ^2 $$
- 解释变量与随机项不相关假设(独立性假设) $$ cov(X_i, ϵ) = 0, i = 1, 2, 3, ···, n $$
- 0 条件均值 $$ E(ϵ|X_i) = 0, i = 1, 2, 3, ···, n $$
0 条件均值是一个放宽的条件,要求误差项在给定所有解释变量条件下的均值为零。由 0 均值可以推出 0 条件均值。 A 和 B 独立的数学定义为: $$ P(A∩B)=P(A)⋅P(B) $$ 根据条件概率公式: $$ P(A∣B)=P(A∩B)/P(B),其中(P(B)>0) $$ 所以在 A 和 B 互相独立的情况下, $$ P(A∣B)=P(A) $$ 计算条件期望, $$ E(ϵ∣X)=∫ϵ⋅f(ϵ∣X)dϵ $$ 由于独立性, $$ f(ϵ∣X)=f(ϵ) $$ 所以, $$ E(ϵ∣X)=∫ϵ⋅f(ϵ)dϵ=E(ϵ)=0 $$ 以上是针对样本总体数据给出的线性假设,但是一般情况下样本总体数据很难获取到,所以可以在总体中随机抽取一部分数据进行参数估计。
给定一组随机抽样数据 $$ {(x_i,y_i)}_{i=1}^n $$ ,假设模型为: $$ yi=β_0+β_1x_i+ϵ_i $$ 其中 ϵi为误差项,满足 $$ E[ϵ_i]=0 $$ 且 $$ Var(ϵ_i)=σ^2 $$ 为了保证我们用这组随机抽样的数据估计出来的参数和整体数据一致,可以采用最小化残差的思路,下面是采用最小二乘法(OLS)估计的过程。
最小二乘法OLS 参数估计 #
最小二乘法目标是最小化残差平方和(RSS),即 $$ RSS = \min_{\beta_0, \beta_1} \sum_{i=1}^n (y_i - \beta_0 - \beta_1 x_i)^2 $$ 是关于 β0 和 β1 的二次函数,其图像是一个开口向上的抛物面(凸函数)。凸函数的驻点(导数为零的点)一定是全局最小值点。对 β0 和 β1分别求偏导,令导数为零可以得到最小值点:
对 β0求偏导 $$ \frac{\partial}{\partial \beta_0} \sum_{i=1}^n (y_i - \beta_0 - \beta_1 x_i)^2 = -2 \sum_{i=1}^n (y_i - \beta_0 - \beta_1 x_i) = 0 $$ 整理得: $$ \sum_{i=1}^n y_i = n \beta_0 + \beta_1 \sum_{i=1}^n x_i \quad \text{(方程1)} $$ 对 β1 求偏导 $$ \frac{\partial}{\partial \beta_1} \sum_{i=1}^n (y_i - \beta_0 - \beta_1 x_i)^2 = -2 \sum_{i=1}^n x_i (y_i - \beta_0 - \beta_1 x_i) = 0 $$ 整理得: $$ \sum_{i=1}^n x_i y_i = \beta_0 \sum_{i=1}^n x_i + \beta_1 \sum_{i=1}^n x_i^2 \quad \text{(方程2)} $$
从方程1解出 β0:
$$ \beta_0 = \frac{1}{n} \left( \sum y_i - \beta_1 \sum x_i \right) = \bar{y} - \beta_1 \bar{x} $$ 其中: $$ \bar{x} = \frac{1}{n} \sum x_i, \quad \bar{y} = \frac{1}{n} \sum y_i $$
将 β0 代入方程2: $$ \left( \bar{y} - \beta_1 \bar{x} \right) \sum x_i + \beta_1 \sum x_i^2 = \sum x_i y_i $$
整理后: $$ \beta_1 \left( \sum x_i^2 - \bar{x} \sum x_i \right) = \sum x_i y_i - \bar{y} \sum x_i $$
最终解: $$ \beta_1 = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2} = \frac{\text{Cov}(X,Y)}{\text{Var}(X)} $$ 显式解 $$ \beta_1 = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2}, \quad \beta_0 = \bar{y} - \beta_1 \bar{x} $$
下面推广到一般,给出最小二乘法的矩阵形式显式解。
最小二乘法的矩阵形式显式解 #
首先需要用到向量的 L2范数(欧几里得范数),对任意向量 $$ v=[v_1,v_2,…,v_n]^⊤ $$ ,其L2范数为: $$ |\mathbf{v}|_2 = \sqrt{v_1^2 + v_2^2 + \cdots + v_n^2} $$ 平方后的L2范数(即L2范数的平方)为: $$ |\mathbf{v}|_2^2 = v_1^2 + v_2^2 + \cdots + v_n^2 = \mathbf{v}^\top \mathbf{v} $$ 残差向量 $$ \mathbf{r} = \mathbf{y} − \mathbf{X}β $$ 表示预测值与真实值的误差。所以L2范数的平方 $$ |\mathbf{r}|_2^2 = r_1^2 + r_2^2 + \cdots + r_n^2 $$ 就是所有样本点的 残差平方和(Sum of Squared Residuals, SSR)。
给定线性回归模型: $$ \mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\epsilon} $$ 其中 ϵ 为误差向量,β 是待估计的参数向量。因为最小二乘法的目标是最小化残差平方和,即: $$ S(\boldsymbol{\beta}) = |\mathbf{y} - \mathbf{X}\boldsymbol{\beta}|_2^2 $$ 我们可以认为这是一个复合函数,它由下面 3 个函数组成 $$ \mathbf{a} = \mathbf{X}\boldsymbol{\beta} $$
$$ \mathbf{b} = \mathbf{y} - \mathbf{a} $$
$$ S(\boldsymbol{\beta}) = |\boldsymbol{b}|_2^2 $$
所以应用链式法则对原函数求偏导可以得到下面的结论, $$ \begin{align*} \frac{\partial S}{\partial \boldsymbol{\beta}} &= \frac{\partial S}{\partial \boldsymbol{\boldsymbol{b}}} \frac{\partial \boldsymbol{b}}{\partial \boldsymbol{\boldsymbol{a}}} \frac{\partial \boldsymbol{a}}{\partial \boldsymbol{\beta}} \ &= \frac{\partial S}{\partial \boldsymbol{\boldsymbol{b}}} \frac{\partial \boldsymbol{(a - y)}}{\partial \boldsymbol{\boldsymbol{a}}} \frac{\partial \boldsymbol{(\mathbf{X}\boldsymbol{\beta})}}{\partial \boldsymbol{\beta}} \ &=2\mathbf{b}^\top \times \mathbf{I} \times \mathbf{X} \ &= 2 (\mathbf{y} -\mathbf{X}\boldsymbol{\beta})^\top \mathbf{X} \end{align*} $$ 令导数等于零, $$ \begin{align*} 2 (\mathbf{y} -\mathbf{X}\boldsymbol{\beta})^\top \mathbf{X} = \mathbf{0}^\top \end{align*} $$ 这里 0⊤ 是一个 1×p 的行向量(p 是参数 β 的维度)。之所以梯度是行向量,是因为损失函数 S 是标量, β 是列向量,标量对列向量的导数是行向量。为了更方便地求解,将方程两边转置可得 $$ \begin{align*}2 \mathbf{X}^\top(\mathbf{y} -\mathbf{X}\boldsymbol{\beta}) = 0\end{align*} $$ 整理得到正规方程: $$ \mathbf{X}^\top\mathbf{X}\boldsymbol{\beta} = \mathbf{X}^\top\mathbf{y} $$ 当 X⊤X 可逆时: $$ \hat{\boldsymbol{\beta}} = (\mathbf{X}^\top\mathbf{X})^{-1}\mathbf{X}^\top\mathbf{y} $$
简单线性回归特例 #
对于 $$ y_i = \beta_0 + \beta_1 x_i + \epsilon_i $$ 的情况: $$ \mathbf{X} = \begin{bmatrix}1 & x_1 \1 & x_2 \\vdots & \vdots \1 & x_n\end{bmatrix}, \quad\boldsymbol{\beta} = \begin{bmatrix}\beta_0 \\beta_1\end{bmatrix} $$ 计算得: $$ \mathbf{X}^\top\mathbf{X} = \begin{bmatrix}n & \sum x_i \\sum x_i & \sum x_i^2\end{bmatrix}, \quad\mathbf{X}^\top\mathbf{y} = \begin{bmatrix}\sum y_i \\sum x_i y_i\end{bmatrix} $$ 最终解得: $$ \hat{\beta}_1 = \frac{n\sum x_i y_i - (\sum x_i)(\sum y_i)}{n\sum x_i^2 - (\sum x_i)^2} \\hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x} $$
无偏性证明 #
下面证明无偏性,即 $$ E(\hat{\boldsymbol{\beta}}) = \boldsymbol{\beta} $$ 证明:
$$ \hat{\boldsymbol{\beta}} = \boldsymbol{\beta} + (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \boldsymbol{\epsilon} $$ 取条件期望: $$ E(\hat{\boldsymbol{\beta}} | \mathbf{X}) = \boldsymbol{\beta} + (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top E(\boldsymbol{\epsilon} | \mathbf{X}) = \boldsymbol{\beta} $$
高斯-马尔可夫定理 #
可以证明,在所有线性无偏估计中,OLS 方差最小。 $$ \text{Var}(\hat{\boldsymbol{\beta}} | \mathbf{X}) = \sigma^2 (\mathbf{X}^\top \mathbf{X})^{-1} $$
正向累积和反向传播 #
上面损失函数的计算图可以用下面的方式来表示
X (n×p) β (p×1)
\ /
\ /
a = Xβ (n×1)
|
y (n×1)|
\ |
b = a - y (n×1)
|
S = bᵀb (标量)
通过这个计算图可以有两种求解的方法,正向累积和反向传播。
正向累积(Forward Accumulation) #
正向累积从输入开始,逐步计算中间变量直至输出。计算图按以下顺序执行 $$ \begin{align*} \boldsymbol{a} &= \mathbf{X}\boldsymbol{\beta} \quad &\text{(矩阵乘法)} \ \end{align*} $$
$$ \begin{align*} \boldsymbol{b} &= \boldsymbol{a} - \mathbf{y} \quad &\text{(残差计算)} \ \end{align*} $$
$$ \begin{align*} S &= |\boldsymbol{b}|^2 = \boldsymbol{b}^\top \boldsymbol{b} \quad &\text{(平方损失)} \end{align*} $$
反向传播(Backward Propagation) #
反向传播从输出开始,利用链式法则计算梯度,逐层传递至输入。 $$ \begin{align*} \frac{\partial S}{\partial \boldsymbol{b}} &= 2\boldsymbol{b}^\top \quad &\text{(标量对向量的导数)} \ \end{align*} $$
$$ \begin{align*} \frac{\partial \boldsymbol{b}}{\partial \boldsymbol{a}} &= \mathbf{I} \quad &\text{(单位矩阵,因 } \boldsymbol{b} = \boldsymbol{a} - \mathbf{y}) \end{align*} $$
$$ \begin{align*} \frac{\partial \boldsymbol{a}}{\partial \boldsymbol{\beta}} &= \mathbf{X}^\top \quad &\text{(矩阵乘法的导数)} \ \end{align*} $$
$$ \begin{align*} \frac{\partial S}{\partial \boldsymbol{\beta}} &= \frac{\partial S}{\partial \boldsymbol{b}} \cdot \frac{\partial \boldsymbol{b}}{\partial \boldsymbol{a}} \cdot \frac{\partial \boldsymbol{a}}{\partial \boldsymbol{\beta}} = 2\boldsymbol{b}^\top \mathbf{I} \mathbf{X} = 2 (\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^\top \mathbf{X} \end{align*} $$
梯度反向传播路径如下,首先给定梯度,然后一步步求接触参数值。
∂S/∂S = 1
|
∂S/∂b = 2bᵀ (1×n)
|
∂b/∂a = I (n×n)
|
∂a/∂β = Xᵀ (p×n)
|
∂S/∂β = 2bᵀX (1×p)
我们用下面的例子来展示反向传播,
import torch
import torchviz
from torch import nn
# 1. 准备数据
n, p = 3, 2 # 样本数3,特征数2
X = torch.tensor([[1.0, 2], [3, 4], [5, 6]], requires_grad=False) # 设计矩阵(3×2)
y = torch.tensor([[3.0], [7], [11]]) # 真实值(3×1)
beta = torch.tensor([[1.0], [2.0]], requires_grad=True) # 待优化参数(2×1)
# 2. 正向计算 (构建计算图)
def forward(X, beta, y):
a = X @ beta # 矩阵乘法 (3×2)(2×1)->(3×1)
b = a - y # 残差计算
S = torch.sum(b ** 2) # 平方损失
return S
S = forward(X, beta, y)
# 3. 可视化计算图 (在backward之前)
graph = torchviz.make_dot(S, params={'β': beta},
show_attrs=True, show_saved=True)
graph.render("least_squares_graph", format="png") # 保存为图片
# 4. 反向传播 (自动微分)
S.backward(retain_graph=True) # 保留计算图
# 5. 验证梯度计算
print("PyTorch计算的梯度:")
print(beta.grad) # 自动微分结果
print("\n公式计算的梯度:")
manual_grad = 2 * (X.t() @ (X @ beta - y)) # 2Xᵀ(Xβ - y)
print(manual_grad)
# 如果需要再次backward,需要重新计算S
# S = forward(X, beta, y)
# S.backward()
下图是生成的计算图的例子,其中最上层蓝色的部分是待训练的参数,ccumulateGrad 是一个关键的反向传播操作节点,它表示梯度累加机制
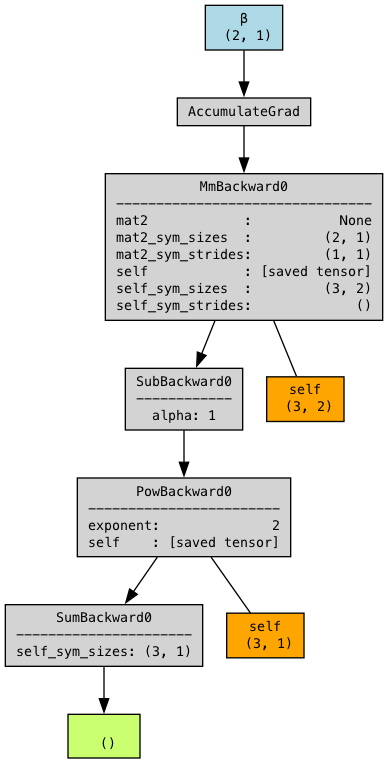
其他变量的含义如下,
a = X @ beta # MatMul: self=X, mat2=beta
b = a - y # Sub: self=a, self=y, alpha=1
S = b.pow(2).sum() # Pow: self=b, exponent=2 → Sum
最后可以运行代码可以得到PyTorch自动微分与数学公式的一致性,

Last modified on 2025-07-06