Skip List | 跳表

Albert Wang / 2024-03-08 / 900 Words/has been Read Times

概念 #

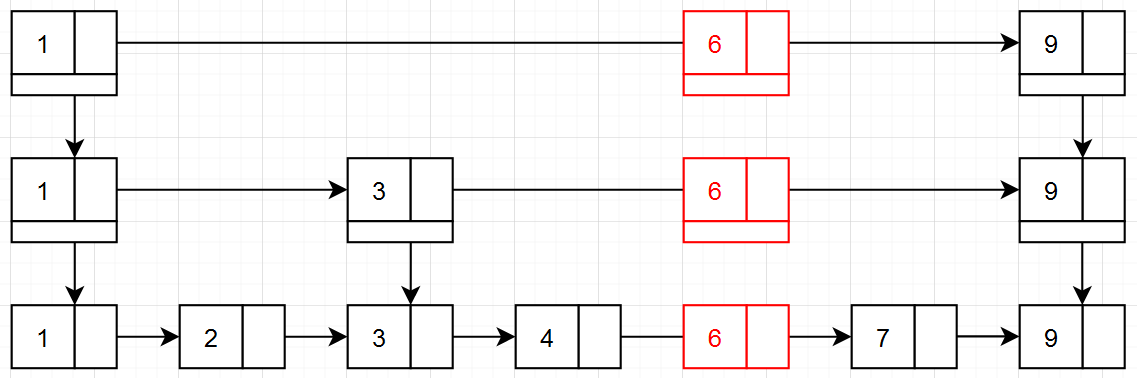
跳表是一种基于链表的动态数据结构，它允许快速地进行查找、插入和删除操作，且实现相对简单。跳表通过在链表的不同层级上建立索引，从而提高了查找效率。跳表的基本思想是在原始链表的基础上建立多层索引，每一层索引都是原始链表的子集，且越高层的索引节点越稀疏。

跳表的节点结构如下面代码中所示，每个节点包含一个键值对以及指向下一层的指针数组，其中 forward[ i ] 表示这个 node 指向跳表第 i 层的下一个节点，也就说说普通的链表 node 都是只有一个 next 节点，而跳表的 node 每一层都有一个 next 节点。跳表的层级是动态的，随着插入操作的进行而逐渐增加。在跳表中，每个节点都包含一个层级属性，表示它在跳表中所处的层数。

#define MAX_LEVEL 6

typedef struct SkipListNode {
    int key;
    int value;
    struct SkipListNode *forward[MAX_LEVEL + 1];
} SkipListNode;

typedef struct SkipList {
    int level;
    SkipListNode *header;
} SkipList;

SkipListNode *createNode(int key, int value, int level) {
    SkipListNode *newNode = (SkipListNode *)malloc(sizeof(SkipListNode));
    newNode->key = key;
    newNode->value = value;
    for (int i = 0; i <= level; i++) {
        newNode->forward[i] = NULL;
    }
    return newNode;
}

SkipList *createSkipList() {
    SkipList *skipList = (SkipList *)malloc(sizeof(SkipList));
    skipList->level = 0;
    skipList->header = createNode(-1, -1, MAX_LEVEL);
    return skipList;
}

跳表的插入操作通过随机生成一个层数，并将新节点插入到对应的层级链表中。

int randomLevel() {
    int level = 0;
    while (rand() < RAND_MAX / 2 && level < MAX_LEVEL) {
        level++;
    }
    return level;
}

下面的代码中 insert 函数首先从最高层开始往下查找，对于第 i 层来说，如果当前节点的 key 小于要插入节点的 key，就在这一层往下查找。这一层最后遍历到的节点的值要么是 NULL，要么 key 的值是第一个大于要插入的 key 的值，同时把这个 key 对应的 node 更新到 update 数组中。

然后调用 randomLevel() 函数得到了新的层数去插入，完整的函数如下：

void insert(SkipList *skipList, int key, int value) {
    SkipListNode *update[MAX_LEVEL + 1];
    SkipListNode *current = skipList->header;

    for (int i = skipList->level; i >= 0; i--) {
        while (current->forward[i] != NULL && current->forward[i]->key < key) {
            current = current->forward[i];
        }
        update[i] = current;
    }
	
    // 这里是指向了第 0 层的数据，也就是真实的数据，其他层都是索引
    current = current->forward[0];

    if (current == NULL || current->key != key) {
        int newLevel = randomLevel();
        if (newLevel > skipList->level) {
            for (int i = skipList->level + 1; i <= newLevel; i++) {
                update[i] = skipList->header;
            }
            skipList->level = newLevel;
        }
        SkipListNode *newNode = createNode(key, value, newLevel);
        for (int i = 0; i <= newLevel; i++) {
            newNode->forward[i] = update[i]->forward[i];
            update[i]->forward[i] = newNode;
        }
    }
}

查找操作从顶层开始，逐层向下查找，直到找到目标节点或者到达最底层。跳表的时间复杂度为 O(log n)，其中 n 表示跳表中的节点数。

SkipListNode *search(SkipList *skipList, int key) {
    SkipListNode *current = skipList->header;
    for (int i = skipList->level; i >= 0; i--) {
        while (current->forward[i] != NULL && current->forward[i]->key < key) {
            current = current->forward[i];
        }
    }
    current = current->forward[0];
    if (current != NULL && current->key == key) {
        return current;
    } else {
        return NULL;
    }
}

为了方便验证，这里增加跳表的打印程序，因为初始化跳表的时候都加了一个值为 -1 的 dummy 节点，所以这里也特别打印出来，以便于理解。

void printSkipList(SkipList *skipList) {
    printf("Skip List:\n");
    for (int i = skipList->level; i >= 0; i--) {
        SkipListNode *current = skipList->header->forward[i];
        printf("Level %d: %-4d", i, -1);
        while (current != NULL) {
            printf("%-4d", current->key);
            current = current->forward[i];
        }
        printf("\n");
    }
}

int main() {
    SkipList *skipList = createSkipList();
    
    insert(skipList, 3, 3);
    insert(skipList, 6, 6);
    insert(skipList, 7, 7);
    insert(skipList, 9, 9);
    insert(skipList, 12, 12);
    insert(skipList, 19, 19);
    insert(skipList, 17, 17);
    insert(skipList, 26, 26);
    insert(skipList, 21, 21);
    insert(skipList, 25, 25);
    insert(skipList, 29, 29);
    insert(skipList, 37, 37);
    insert(skipList, 31, 31);
    insert(skipList, 42, 42);
    insert(skipList, 39, 39);
    insert(skipList, 49, 49);
    insert(skipList, 46, 46);
    insert(skipList, 38, 38);

    printSkipList(skipList);

    return 0;
}

然后构造测试用例，执行效果如下：

然后我们站在巨人的肩膀上了解一下 leveldb 中关于跳表的实现。

leveldb 跳表实现 #

Leveldb 本身是一个基于 LSM tree 的 KVDB，其中调表是它 memtable 在内存中的存放方式，它的源代码位于(https://github.com/google/leveldb/blob/main/db/skiplist.h)。

首先Node 结构和 SkipList 模板类如下， Node 本身用了 explicit 修饰，防止隐式转换。next_[1] 实际会根据节点高度动态分配更大空间。

Leveldb 本身实现了内存池 Arena，这里不做过多介绍。

struct Node {
  explicit Node(const Key& k) : key(k) {}
  Key const key;  // 不可变的键值
  std::atomic<Node*> next_[1];  // 柔性数组，存储各级指针
};

template <typename Key, class Comparator>
class SkipList {
 private:
  enum { kMaxHeight = 12 };  // 最大高度限制
  Node* const head_;  // 头节点
  std::atomic<int> max_height_;  // 当前最大高度
  Random rnd_;  // 随机数生成器
};

template <typename Key, class Comparator>
SkipList<Key, Comparator>::SkipList(Comparator cmp, Arena* arena)
    : compare_(cmp),
      arena_(arena),
      head_(NewNode(0 /* any key will do */, kMaxHeight)),
      max_height_(1),
      rnd_(0xdeadbeef) {
  for (int i = 0; i < kMaxHeight; i++) {
    head_->SetNext(i, nullptr);
  }
}

节点查找 - FindGreaterOrEqual() #

找到第一个键值 ≥ 目标值的节点。

从最高层开始搜索
在当前层向右移动，直到下一个节点的键值 ≥ 目标值
记录每层的前驱节点到 prev 数组（用于插入）
下降到下一层继续搜索
到达第 0 层时返回找到的节点

template <typename Key, class Comparator>
typename SkipList<Key, Comparator>::Node*
SkipList<Key, Comparator>::FindGreaterOrEqual(const Key& key,
                                              Node** prev) const {
  Node* x = head_;
  int level = GetMaxHeight() - 1;
  while (true) {
    Node* next = x->Next(level);
    if (KeyIsAfterNode(key, next)) {
      // Keep searching in this list
      x = next;
    } else {
      if (prev != nullptr) prev[level] = x;
      if (level == 0) {
        return next;
      } else {
        // Switch to next list
        level--;
      }
    }
  }
}

节点插入 - Insert() #

查找插入位置：获取每层的前驱节点，并确认没有重复键
确定新节点高度：以 1/4 的概率增加高度（kBranching = 4）
更新最大高度：如果新节点高度超过当前最大高度，更新 max_height_ 并设置高层前驱为头节点
链接新节点：

当设置 x->next_[i] 时，节点 x 还未对其他线程可见。

只有当我们通过 prev[i]->SetNext(i, x) 发布节点 x 时，才需要内存屏障，在这之前使用无屏障操作是安全的

template <typename Key, class Comparator>
void SkipList<Key, Comparator>::Insert(const Key& key) {
  Node* prev[kMaxHeight];
  Node* x = FindGreaterOrEqual(key, prev);

  // Our data structure does not allow duplicate insertion
  assert(x == nullptr || !Equal(key, x->key));

  int height = RandomHeight();
  if (height > GetMaxHeight()) {
    for (int i = GetMaxHeight(); i < height; i++) {
      prev[i] = head_;
    }
    max_height_.store(height, std::memory_order_relaxed);
  }

  x = NewNode(key, height);
  for (int i = 0; i < height; i++) {
    x->NoBarrier_SetNext(i, prev[i]->NoBarrier_Next(i));
    prev[i]->SetNext(i, x);
  }
}

高度随机化 - RandomHeight() #

template <typename Key, class Comparator>
int SkipList<Key, Comparator>::RandomHeight() {
  static const unsigned int kBranching = 4;
  int height = 1;
  while (height < kMaxHeight && rnd_.OneIn(kBranching)) {
    height++;
  }

  return height;
}

高度为 1 的概率：P(h=1) = 3/4 = 0.75
高度为 2 的概率：P(h=2) = (1/4) × (3/4) = 3/16 = 0.1875
高度为 3 的概率：P(h=3) = (1/4)² × (3/4) = 3/64 = 0.046875
高度为 4 的概率：P(h=4) = (1/4)³ × (3/4) = 3/256 = 0.01171875
…
高度为 kMaxHeight(12) 的概率：P(h=12) = (1/4)^11 = 很小

LevelDB 选择 4 的原因：

减少指针内存占用，搜索性能降低不多（log₄n = ½ log₂n，只差常数因子）

分支因子	期望高度	平均指针数	搜索比较次数
2	log₂n	n 个节点 ≈ 2n 指针	较少
4	log₄n	n 个节点 ≈ 1.33n 指针	稍多
8	log₈n	n 个节点 ≈ 1.14n 指针	更多

Last modified on 2026-01-24