对于下面这个 3 * 3 的矩阵来说,如果我们想要从从左上角走到右下角,每次只能走一步,问怎么走距离最短。
假如现在有一个问题,对于下面这个 3 * 3 的矩阵来说,如果我们想要从从左上角走到右下角,每次只能走一步,问怎么走距离最短?
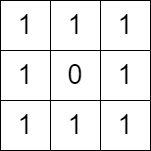
这个题目我们一般就直接采用 BFS 计算出结果,这样做无疑是最方便的。但是我们同样可以先构建图,然后再使用 dijkstra 算法来计算最小路径。上面的矩阵可以被表示为下面这样的一张图,
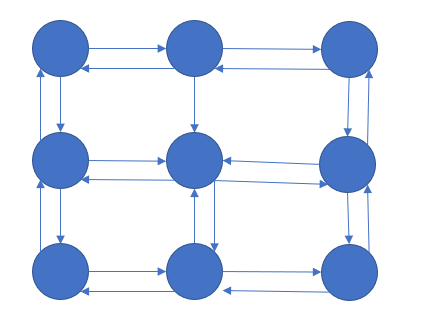
但是我们用邻接表表示这张图就稍微有点困难了,因为一般来说我们表示图的某一个节点一般是用一个数字 i ( 0 <= i < n) 来表示的,但是这回的顶点确是用(i, j)这一个点对来表示的。所以我们邻接表的数据结构用数组 + 链表就不太方便了,这时可以用 Map 来表示。
在 Java 语言的实现中一般是要用 HashMap,这时就要考虑可能出现哈希碰撞的情况,比较有效的一个办法是重写 hashCode 函数,如下图中的 Pair 对象。关于为什么要重写 hashCode 函数可以参考我这篇博客 。
class Pair {
int x;
int y;
int distance;
public Pair(int x, int y, int distance) {
this.x = x;
this.y = y;
this.distance = distance;
}
public int hashCode() {
return (x << 16) | y;
}
public boolean equals(Object a) {
Pair obj = (Pair)a;
if (obj == null) {
return false;
}
return this.x == obj.x && this.y == obj.y;
}
}
然后就是建图的过程了,这个和一维的比较类似,这里不多阐述。
public void addEdge(HashMap<Pair, List<Pair>> graph, Pair a, Pair b, int m, int n) {
if (a.x < 0 || a.x >= m || a.y < 0 || a.y >= n) {
return;
}
List<Pair> list = graph.getOrDefault(a, null);
if (list == null) {
list = new ArrayList<>();
}
list.add(b);
graph.put(a, list);
}
public int init(int[] start, int[] target) {
int m = target[0] + 1;
int n = target[1] + 1;
HashMap<Pair, List<Pair>> graph = new HashMap<>();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
Pair b = new Pair(i, j, 1);
addEdge(graph, new Pair(i - 1, j, 1), b, m, n);
addEdge(graph, new Pair(i + 1, j, 1), b, m, n);
addEdge(graph, new Pair(i, j + 1, 1), b, m, n);
addEdge(graph, new Pair(i, j - 1, 1), b, m, n);
}
}
return dijkstra(graph, new Pair(start[0], start[1], 1), new Pair(target[0], target[1], 1), m, n);
}
需要注意的是在 Pair 对象的创建中我们都要初始化一个从 a 点到 b 点的距离。比如下面的代码表示添加一条从 a 到 b 的边,这条边的权重是 1,由 b 这个对象的 distance 字段来表示。这里 a 的 distance 字段可以填任意值,因为我们重写了 Pair 的 equals 函数,比较两个对象是否相同的时候只会比较它们是否表示了同一个点。
Pair a = new Pair(i - 1, j, 1);
Pair b = new Pair(i, j, 1);
addEdge(graph, a, b, m, n);
下面是 dijkstra 的实现,仅供参考。
public int dijkstra(HashMap<Pair, List<Pair>> graph, Pair start, Pair end, int m, int n) {
int[][] distance = new int[m][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
distance[i][j] = Integer.MAX_VALUE;
}
}
distance[start.x][start.y] = 0;
PriorityQueue<Pair> pq = new PriorityQueue<>((a, b) -> (a.distance - b.distance));
pq.add(new Pair(start.x, start.y, 0));
while (!pq.isEmpty()) {
Pair cur = pq.poll();
if (distance[cur.x][cur.y] != cur.distance) { // 已经是固定标号点要退出
continue;
}
List<Pair> list = graph.get(cur);
for (int i = 0; i < list.size(); i++) {
Pair pair = list.get(i);
if (distance[cur.x][cur.y] + pair.distance < distance[pair.x][pair.y]) {
distance[pair.x][pair.y] = distance[cur.x][cur.y] + pair.distance;
pq.add(new Pair(pair.x, pair.y, distance[cur.x][cur.y] + pair.distance));
}
}
}
return distance[end.x][end.y] == Integer.MAX_VALUE ? -1 : distance[end.x][end.y];
}
Last modified on 2023-05-02