DFS and BFS with Graph | 无向图深度优先与广度优先

背景 #

我们来看这样一道经典的题目，一个矩阵中有 0 和 1 两种元素，现在要从左上角开始遍历，每次可以选择八个方向，并且只能访问值为 0 的节点，问它最短需要走多少步才能到达，查看原题可以点击这里 。

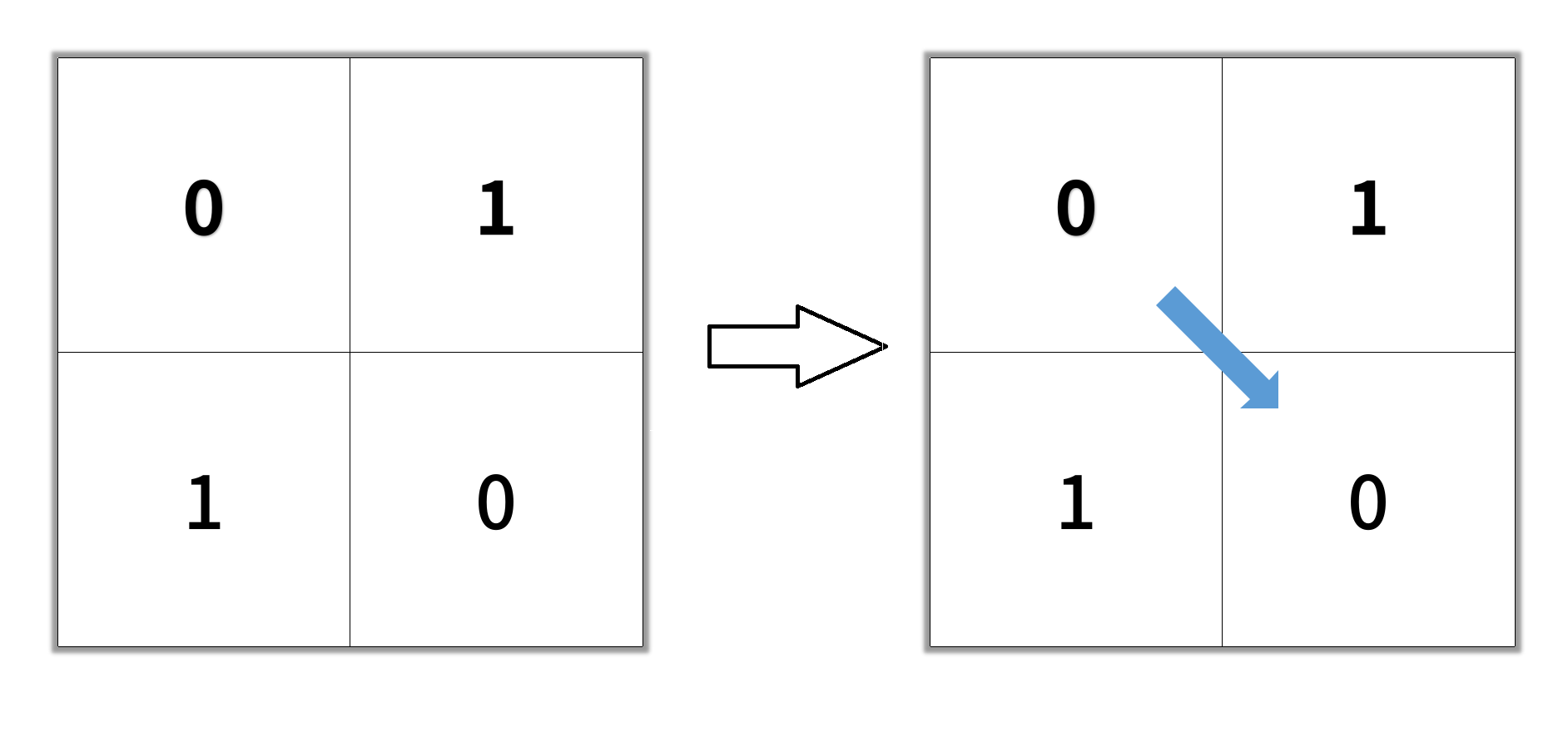
这就是一个非常典型的遍历无向图的例子了，下面我们分别介绍 DFS 和 BFS 需要注意些什么。

DFS #

我们先假设在上图中机器人先选择向下走了一步，然后它就到了（1，0）这个点，在这个点上它可以选择向任意四个方向前进，但是又不能走出去，所以它可选的方向就只有三个，分别是向下，向右和向上。假如它选择了向上，那它就又回到了（0，0）这个点，当它回到原点之后它有可以选择来到（1，0），这样重复之后程序就永远不可能会退出了。

针对这种情况我们来思考一下解决办法，之所以出现这种情况，是因为它走了重复的路。而它一旦走了重复的路，那这条路必然就不可能是最短的路，所以我们要禁止这种情况的发生。代码里通常有两种做法来避免这种情况的发生，一种是很直观的禁止它走“回头路”，代码实现如下

class Solution {
    int ans;
    int[][] paths = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};
    boolean[][] isVisited;

    public boolean valid(int[][] grid, int x, int y) {
        if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length) {
            return false;
        }

        if (isVisited[x][y] || grid[x][y] == 1) {
            return false;
        }

        return true;
    }

    public void backtrack(int[][] grid, int x, int y, int cnt) {
        if (!valid(grid, x, y)) {
            return;
        }

        cnt++;
        if (x == grid.length - 1 && y == grid[0].length - 1) {
            ans = Math.min(ans, cnt);
            return;
        }

        for (int[] path : paths) {
            int newX = x + path[0];
            int newY = y + path[1];
            isVisited[x][y] = true;
            backtrack(grid, newX, newY, cnt);
            isVisited[x][y] = false;
        }
    }

    public int shortestPathBinaryMatrix(int[][] grid) {
        ans = Integer.MAX_VALUE;
        isVisited = new boolean[grid.length][grid[0].length];
        
        backtrack(grid, 0, 0, 0);

        if (ans == Integer.MAX_VALUE) {
            return -1;
        }
        return ans;
    }
}

上面代码中的 isVisited 数组就是用来防止代码走回头路的，如果某个点已经被访问过了，那就直接返回。这种做法要面临的一个问题是我们需要额外的 m * n 空间来存储某个点是否被访问过，空间复杂度比较高，可以用下面这种方式优化一下

BFS #

上面的 DFS 实现是要不断地压栈递归遍历的，这种情况导致的问题是一旦数据量稍微大一点就可能导致栈溢出。所以我们可以用 BFS 来做这道题。通常有一些经验的做法，假如题目要求的是最短路径，那一般可以用 BFS，如果是要遍历所有可能的路径，那可以用 DFS。DFS 的代码实现如下：

class Solution {
    int ans;
    int[][] paths = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}, {1, 1}, {1, -1}, {-1, 1}, {-1, -1}};

    public int shortestPathBinaryMatrix(int[][] grid) {
        if (grid[0][0] == 1) {
            return -1;
        }

        Queue<Pair> que = new LinkedList<>();
        que.add(new Pair(0, 0, 0));

        while (!que.isEmpty()) {
            Pair pair = que.poll();
            int x = pair.x;
            int y = pair.y;
            int newCnt = pair.cnt + 1;

            if (x == grid.length - 1 && y == grid[0].length - 1) {
                return newCnt;
            }

            for (int[] path : paths) {
                int newX = x + path[0];
                int newY = y + path[1];
                
                if (newX < 0 || newX >= grid.length || newY < 0 ||
                    newY >= grid[0].length || grid[newX][newY] == 1) {
                    continue;
                }
  
                que.add(new Pair(newX, newY, newCnt));
                grid[newX][newY] = 1;
            }
        }

        return -1;
    }
}

class Pair {
    int x;
    int y;
    int cnt;

    public Pair(int x, int y, int cnt) {
        this.x = x;
        this.y = y;
        this.cnt = cnt;
    }
}

观察代码我们可以发现 DFS 和树的广度优先遍历非常像，因为树本身就是一个无环的连通图，所以实现上都很相似。

Last modified on 2023-05-01