在几个月前我总结了图最短路问题常用的几个算法以及实现 。但是随后我就发现了一个很大的问题,之前算法的实现都是采用的邻接矩阵,这种实现方式最大的问题就是太占用内存空间。假如一个稀疏图有 n 个顶点,m 条边(其中 m « n),在这种情况下用邻接矩阵来表示图需要的内存空间是$O(n^2)$,在一些算法题中 n 的数量往往会达到 $10^5$,而给定的内存范围是 $10^9$,这就导致临界矩阵往往不能用来做这些图的题目。如果采用邻接表来表示一个图只需要 $O(n + m)$ 的内存空间,所以下面我们用邻接表来实现Dijkstra 算法。
首先我们来构造图,代码如下。其中 n 表示有 n 个节点,并且节点的值为 0 ~ n - 1,edges 表示边的集合,edge[0]和edge[1]表示从 edge[0] 到 edge[1] 有边,edge[2] 表示这条边的权重。
public int init(int n, int[][] edges) {
ArrayList<Node>[] graph = new ArrayList[n];
for (int i = 0; i < n; i++) {
graph[i] = new ArrayList<>();
}
for (int[] edge : edges) {
graph[edge[0]].add(new Node(edge[1], edge[2]));
graph[edge[1]].add(new Node(edge[0], edge[2])); // 无向图
}
return dijkstra(graph, 0, n - 1, n);
}
为了同时表示边和权重,这里用一个 Node 对象,其中 id 表示到节点 id 的边,distance 表示权重。
class Node {
int id;
int distance;
public Node(int id, int distance) {
this.id = id;
this.distance = distance;
}
}
然后使用邻接表来实现 dijkstra 算法,
public int dijkstra(ArrayList<Node>[] graph, int start, int end, int n) {
int[] distance = new int[n];
for (int i = 0; i < n; i++) {
distance[i] = Integer.MAX_VALUE;
}
distance[start] = 0;
PriorityQueue<Node> pq = new PriorityQueue<>((a, b) -> (a.distance - b.distance));
pq.add(new Node(start, 0));
while (!pq.isEmpty()) {
Node cur = pq.poll();
if (distance[cur.id] != cur.distance) { // 已经是固定标号点要退出
continue;
}
ArrayList<Node> list = graph[cur.id];
for (int i = 0; i < list.size(); i++) {
Node y = list.get(i);
if (distance[cur.id] + y.distance < distance[y.id]) {
distance[y.id] = distance[cur.id] + y.distance;
pq.add(new Node(y.id, distance[cur.id] + y.distance));
}
}
}
return distance[end] == Integer.MAX_VALUE ? -1 : distance[end];
}
下面我们来看一下这段代码的实现细节。首先这里采用堆来保证依次选择距离的最小值。因为每次迭代都是选择临时标号点,所以在上面的代码中用了下面的判断来剔除固定标号点。
if (distance[cur.id] != cur.distance) { // 已经是固定标号点要退出
continue;
}
然后我们开始遍历与该节点相邻的每一条边,如果发现 distance[cur.id] + y.distance < distance[y.id] 就更新 从 start到 distance[y.id]的距离。
ArrayList<Node> list = graph[cur.id];
for (int i = 0; i < list.size(); i++) {
Node y = list.get(i);
if (distance[cur.id] + y.distance < distance[y.id]) {
distance[y.id] = distance[cur.id] + y.distance;
pq.add(new Node(y.id, distance[cur.id] + y.distance));
}
}
下面我们来考虑一下怎么用 dijkstra 算法来计算一个图中的最短环。我们先来思考假如图中有环会怎么样,如下图所示
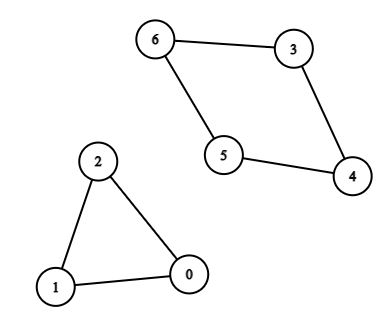
假如一个图有环,那它必然存在两个节点A,B,使得从节点A到节点B是有边的,同时删除A和B之间的这条边,A和B依然是连通的。比如上图中的 6 和 3 这两个节点,从 6 到 3 存在一条边,并且删除这条边,依然存在这一条路径使得节点 6 和 3 连通。
所以我们在 dijkstra 算法里可以加入一条判断,剔除从 A 到 B 的边,然后求从 A 到 B 的最短路径。代码如下
ArrayList<Node> list = graph[cur.id];
for (int i = 0; i < list.size(); i++) {
Node y = list.get(i);
if ((cur.id == start && y.id == end) ||
(cur.id == end && y.id == start)) { // 剔除从 A 到 B 的边
continue;
}
if (distance[cur.id] + y.distance < distance[y.id]) {
distance[y.id] = distance[cur.id] + y.distance;
pq.add(new Node(y.id, distance[cur.id] + y.distance));
}
}
如果最终返回的最短路径是有效的,表示从 A 到 B 存在一条环。
Last modified on 2023-04-22