问题背景 #
假设我们有下面这张图,图中边的权重表示两点之间的距离。我们希望找到一条最短的路径从这张图的 A 点出发,最终走到 E 点,该怎样考虑这个问题呢?
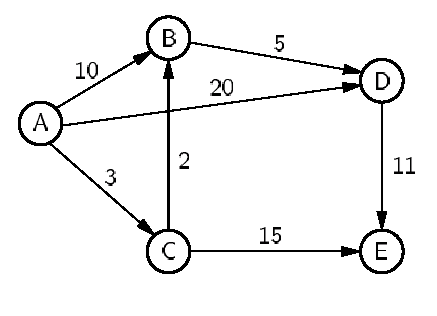
这个问题很具有现实的意义,假设两点表示两个城市的距离,我们往往希望能够走最短距离的那条路到达目的地。而且这个问题也有一个隐含的条件,那就路的距离不可能为负数,所以我们可以考虑使用 Dijkstra 算法来进行求解。
Dijkstra 算法 #
Dijkstra 算法考虑对每一个点进行标号,每个点对应着两种状态(固定标号和临时标号,表示已经确定最短路径和尚未确定),一开始只有出发点的状态是已经确定最短路径的,然后会在迭代的时候去更新标号点,同时也会对每个点的最短路径进行更新。
图表模拟 #
下面我们先用图表的方式来进行模拟 Dijkstra 的求解过程。首先我们用一个数组来存储每个点的状态,最开始只有 A 点的状态是确定的,A 点到 A 点的距离初始化为 0,然后初始化 A 点到其余各点的距离,如果 A 点到某一个点没有路径,则初始化为无穷大。从 A 点开始迭代,更新 A 点到到各点的最短距离,如下图所示
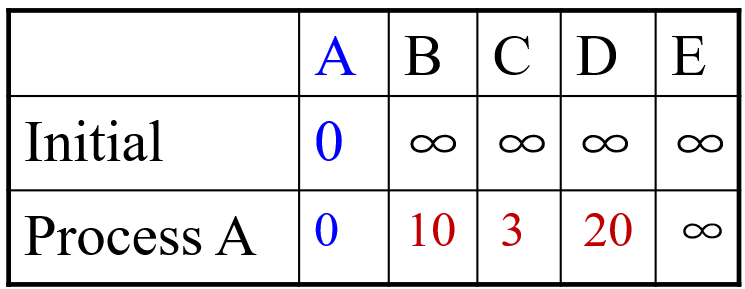
这时我们能确定 A 点到 C 点的最短距离是 3,然后就将 C 点的状态设置为确定,再从 C 点开始迭代,继续更新到其余未确定点之间的最小距离,如下图
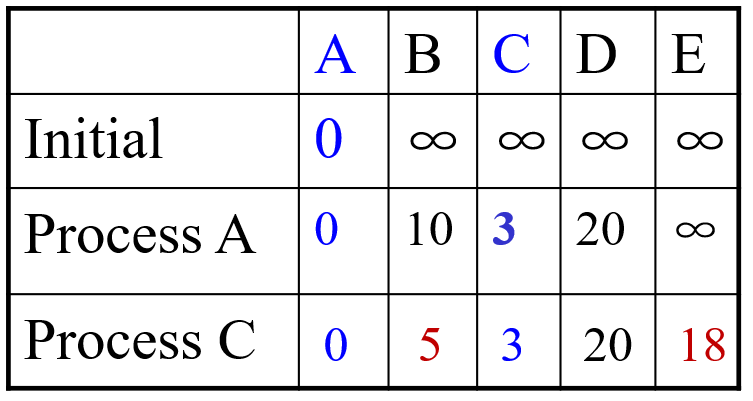
这时我们确定了,A 点到 B 点的最短距离是 5,然后将 B 点设置为确定,再更新其他未确定的点。直到最终目的地的点被标注为已确定,如下图所示
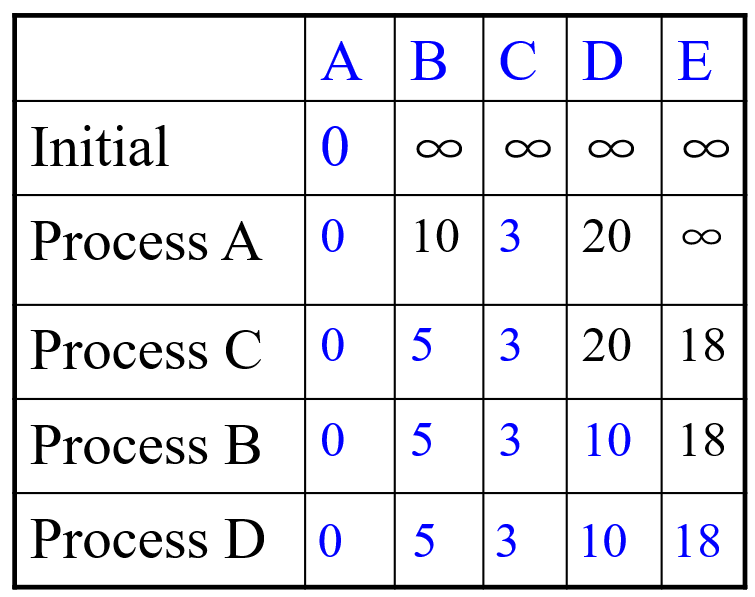
这样我们就得到了 A 点到 E 点的最短路径 18. 下面我们用代码来实现上面的算法。
代码实现 #
我们采用邻接矩阵来实现 dijkstra 算法
#include <stdlib.h>
#include <stddef.h>
#include <stdio.h>
#include <string.h>
#define INF 10000001
#define N 101
int graph[N][N];
void dijkstra(int *distance, int *flag, int n)
{
int a, b;
for (int i = 0; i < n - 1; i++) {
a = -1;
b = INF;
for (int j = 1; j < n; j++) { // 找出发点到 j 点的最小距离
if (flag[j] == 0 && distance[j] < b) {
a = j;
b = distance[j];
}
}
if (a == -1) { // 没有路到终点
break;
}
if (a == n - 1) { // 已经找到了到终点的最短路
break;
}
flag[a] = 1; // 改为固定标号
for (int j = 1; j < n; j++) {
if (flag[j] == 0 && (b + graph[a][j] < distance[j])) {
distance[j] = b + graph[a][j];
}
}
}
if (distance[n - 1] >= INF) {
printf("Impossible!\n");
} else {
printf("%d\n", distance[n - 1]);
}
}
int main()
{
int a, b, c, n, m;
int distance[N] = {0}; // 起点到该点的最短距离
int flag[N] = {0}; // 固定标号与临时标号
scanf("%d%d", &n, &m); // n 个点, m 条边
// 初始化各个数据结构
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
if (i == j) {
graph[i][j] = 0;
} else {
graph[i][j] = INF;
}
}
}
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &a, &b, &c);
a--;
b--; // 假设输入的图节点是从下标 1 开始
graph[a][b] = c;
// graph[b][a] = c; // 如果是无向图
}
for (int i = 1; i < n; i++) {
distance[i] = graph[0][i];
}
flag[0] = 1; // 初始只有起点是固定标号
dijkstra(distance, flag, n);
}
最开始的图可以按照下面的方式输入,然后就能得到最短路径 18.
5 6
1 2 10
1 3 3
1 4 20
2 4 5
3 5 15
4 5 11

Bellman-Ford 算法 #
大家可能注意到了在上面的代码中我们是按照节点进行遍历的,Bellman-Ford 算法则是按照边来进行遍历的。之所以能这么做是因为下面的条件,
- 如果最短路存在,则最短路经过的边数不超过 n - 1 条;
- 当负权存在时,最短路都不一定存在(有负环时一定不存在)。
然后我们的核心代码可以这样进行修改,将原来的邻接矩阵换成边的数组,然后我们就可以根据上面的条件控制遍历次数在 n - 1 次。distance[i] 依然表示从出发点到 i 点的最短距离。
if (distance[edge[i].v] > distance[edge[i].u] + edge[i].w) {
distance[edge[i].v] = distance[edge[i].u] + edge[i].w;
}
上面这段代码表示如果直接从出发点到 v 点的距离大于先从出发点到 u 点,再从 u 点到 v 点的距离,就对 distance 数组进行更新
#include <stdio.h>
#include <stdbool.h>
#define INF 10000001
#define N 101
typedef struct Edge_ {
int u;
int v;
int w;
} Edge;
void bellmanFord(int *distance, Edge *edge, int n, int m)
{
bool flag;
for (int k = 0; k < n - 1; k++) {
flag = false;
for (int i = 0; i < m; i++) {
if (distance[edge[i].v] > distance[edge[i].u] + edge[i].w) {
distance[edge[i].v] = distance[edge[i].u] + edge[i].w;
}
}
if (!flag) {
break;
}
}
// 检测负权回路
flag = false;
for (int i = 0; i < m; i++) {
if (distance[edge[i].v] > distance[edge[i].u] + edge[i].w) {
flag = true;
break;
}
}
if (flag) {
printf("该图有负权回路\n");
} else {
printf("%d\n", distance[n - 1]);
}
}
int main()
{
int a, b, c, n, m;
int distance[N] = {0}; // 起点到该点的最短距离
Edge edge[N] = {0};
scanf("%d%d", &n, &m); // n 个点, m 条边
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &a, &b, &c);
a--; b--;
edge[i].u = a;
edge[i].v = b;
edge[i].w = c;
}
for (int i = 1; i < n; i++) {
distance[i] = INF;
}
bellmanFord(distance, edge, n, m);
}
用 Bellman-Ford 算法我们同样可以得到最短路径 18.

Floyd 算法 #
如果我们要求任意两点之间的距离,用 Dijkstra 算法可能需要调用 n 次,这时用 Floyd 算法就可以很好地解决这个问题。Floyd 算法利用了动态规划的思想,它的状态转移方程可以用下面的方式表达。 $$ d[i][j] = min(d[i][j], d[i][k] + d[k][j]), 其中 0 <= i, j, k < n $$ 其核心思想也就是说如果直接从 i 点到 j 点的距离小于先从 i 点到 k 点,再从 k 点到 j 点,那我们就要选择距离最小的点。
Floyd 算法的代码实现如下,它的代码实现相对与前面两个算法来说更为简单一些,也更容易记忆,建议优先掌握 Floyd 算法。
#include <stdio.h>
#include <stdbool.h>
#define INF 10000001
#define N 101
int graph[N][N];
void floyd(int n)
{
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (graph[i][j] > graph[i][k] + graph[k][j]) {
graph[i][j] = graph[i][k] + graph[k][j];
}
}
}
}
printf("%d\n", graph[0][n - 1]);
}
int main()
{
int a, b, c, n, m;
scanf("%d%d", &n, &m); // n 个点, m 条边
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j) {
graph[i][j] = 0;
} else {
graph[i][j] = INF;
}
}
}
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &a, &b, &c);
a--; b--;
graph[a][b] = c;
}
floyd(n);
}
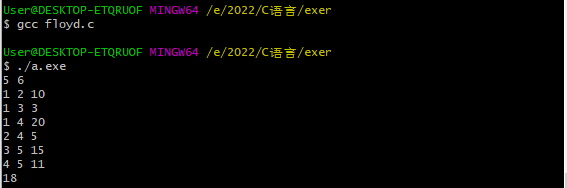
Floyd 算法的测试结果如下:
Last modified on 2023-01-07