戈尼斯堡七桥问题 #
我们先来看一个经典问题。假如有两座小岛,大的小岛和旁边的陆地有四座桥相连,小的岛和陆地有两座桥相连,两个小岛之间有一座桥相连。相当于说有四座陆地,七座桥,问从任何一块陆地出发,每座桥只走一次,最终能否回到原点。类似的问题是一笔画问题(从某一个点出发,不能提起笔,问最终能否回到原点)。
我们可以把上面的问题抽象成右上角所示的图模型,点表示陆地,连线表示桥,这就构成了一个图模型。我们现在来考虑怎么对这个模型进行表达。
图的表示 #
对于上面的这个图模型来说,我们从数学上可以得到三个集合,点的集合V(G),边的集合E(G)和边到实数的一个映射函数F(G)(通常表示权重)。在计算机中则是主要通过邻接矩阵和邻接表这两种方式来表示图。
邻接矩阵 #
邻接矩阵是一个二维的方阵,其中 matrix[i] [j] 用来表达节点 i 和节点 j 是否关联。在图初始化的时候通常以二维数组的方式作为输入,其中第二维表示两个节点和节点之间的关系,比如下面的这个输入就表示节点 1 和节点 2 之间是有边的,并且边的权重为 10。在有些情况下权重是可以忽略的,我们更关心节点间是否连通。
1 2 10
为了符合人类的思考方式,往往节点坐标都是从 1 开始的,这里我们也先假设点的坐标是从 1 开始,然后给出邻接矩阵的实现代码。
#define MAX_SIZE 100
int main()
{
int n, m, u, v;
int matrix[MAX_SIZE][MAX_SIZE] = {0};
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%d%d", &u, &v);
matrix[u - 1][v - 1] = 1;
matrix[v - 1][i - 1] = 1; // 无向图的连接方式
}
return 0;
}
如果边是有权的,我们在最初赋值的时候会给定一个无穷大的值表示不可访问,如果i == j ,权值为 0。
#define MAX_SIZE 100
#define INF 10000001
int main()
{
int n, m, u, v, w;
int matrix[MAX_SIZE][MAX_SIZE];
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i == j) {
matrix[i][j] = 0;
} else {
matrix[i][j] = INF;
}
}
}
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &u, &v, &w);
matrix[u - 1][v - 1] = w;
matrix[v - 1][i - 1] = w; // 无向图的连接方式
}
return 0;
}
现在我们已经有了数据结构的表达,然后再加上一定算法来对这个数据结构进行操作就是我们写程序的目的。通常用到的算法就是深度优先遍历和广度优先遍历。下面就是一个深度优先遍历的例子,用递归的方式实现。
int isVisisted[MAX_SIZE] = {0};
void dfs(int i, int **matrix, int n)
{
isVisisted[i] = 1;
for (int j = 0; j < n; j++) {
if (!isVisisted[j] && matrix[i][j] != 0) {
dfs(j, matrix, n);
}
}
}
这个操作的时间复杂度和空间复杂度都为$O(n^2)$。
邻接表 #
邻接矩阵处理稀疏图的效率比较低,处理含有平行边的图也不太方便,邻接表则能很好弥补这一不足。为了代码编写方便,下面我们假设点是从 0 开始的。下面的代码是邻接表实现的例子
typedef struct Edge_ {
int nodeId;
int edgeValue;
struct Edge_ *next;
} Edge;
typedef struct Node_ {
Edge *next;
} Node;
void init(int u, int v, int w, Node *node)
{
Edge *edge = (Edge *)malloc(sizeof(Edge));
edge->nodeId = v;
edge->edgeValue = w;
edge->next = node[u].next;
node[u].next = edge; // 头插法
}
int main()
{
int n, m, u, v, w;
Node node[MAX_SIZE] = {0};
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &u, &v, &w);
init(u, v, w, node);
init(v, u, w, node); // 无向图
}
}
邻接表的时间复杂度是$O(n + m)$,
邻接表还可以用多个一维数组来实现,我们可以把 Edge 的元素都存在单独的数组里,如下图所示

针对有向图的代码实现如下
int main()
{
int n, m, u, v, w;
int node[MAX_SIZE];
memset(node, -1, sizeof(node));
int nodeId[MAX_SIZE];
memset(nodeId, -1, sizeof(nodeId));
int edgeValue[MAX_PATH] = {0};
int next[MAX_SIZE];
memset(next, -1, sizeof(next));
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i++) {
scanf("%d%d%d", &u, &v, &w);
nodeId[i] = v; // 针对有向图
next[i] = node[u];
node[u] = i;
}
dfs(node, nodeId, next, n);
}
它的深度优先遍历方式如下
void dfs(int *node, int *nodeId, int *next, int n)
{
for (int i = 0; i < n; i++) {
int e = node[i];
while ( e != -1) {
if (!isVisisted[nodeId[e]]) {
printf("%d ", nodeId[e]);
}
isVisisted[nodeId[e]] = 1;
e = next[e];
}
printf("\n");
}
}
欧拉图 #
了解到图在计算机中的表示之后,我们继续回到原来的问题。戈尼斯堡七桥问题最先是由欧拉解决的,所以假如存在一条回路可以解决上述的问题,我们就称这条回路为欧拉回路,这个图就叫欧拉图。有些图不一定存在这样的回路,但是有可能它存在一条通路,使得每个边恰好只走一次,这样的通路就叫欧拉通路。对于戈尼斯堡七桥问题,我们还需要人为定义度的概念。
- 在无向图中,度表示有多少条边和这个节点关联。特别地,自环算两度;
- 在有向图中,度分为入度和出度,入度表示进入这个节点的边数(有多少歌箭头指向它),出度表示从这个节点出发的边数。
然后欧拉得到了这样的结论,
- 如果无向图所有顶点度数都是偶数,那一定会存在欧拉回路;如果有向图所有顶点的入度等于出度,则一定存在欧拉回路。
- 如果无向图存在欧拉通路,那么这个图一定恰好存在两个奇度数节点,我们可以从其中一个奇度数节点出发,从另一个奇度数节点出来;如果有向图恰好有一个节点的出度比入读多1,另一个节点的出度比入度少1,其他节点出度和入读数相等,则必然存在欧拉通路。
欧拉给出的解决问题的办法是让我们去判断这个无向图所有顶点度数是不是都为偶数,这种做法很容易去实现,下面我们给出求一个无向图度的代码,其中参数 i 表示是第 i 个节点,n 表示总共有 n 个节点。
int getDeg(int i, int n) { //求度数
int cnt = 0;
for (int j = 0; j < n; j++) {
if (i == j) {
continue;
}
if (matrix[i][j] || matrix[j][i]) {
cnt++;
}
}
return cnt;
}
根据上面的代码我们就可以求出每一个节点的度数,然后去深度优先遍历所有的节点(加上isVisisted数组)。判定条件为是否有节点没有被遍历到(不连通)或者有节点的度数不是偶数(不能构成欧拉回路)。
下面我们换一种思路来理解“所有顶点度数都为偶数”这句话。我们先假设这个条件成立,即图中所有顶点度数都为偶数。然后如果我们在图中随便找一个回路,把这个回路中的边从图中剔除掉,这时图中的所有节点的度数仍然是偶数。然后我们就能继续这个过程,再找一条回路,再把所有的边剔除,最终这个图中的边就会被我们完全剔除,也就相当于完成了遍历。
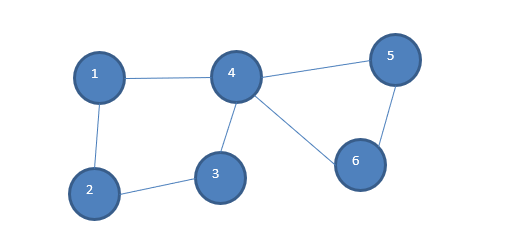
这里给出深度优先的解法,我们去遍历所有的边,并且每条边只遍历一次,在存在欧拉回路的情况下我们可以求出一条遍历的路径出来。最后我们可以通过 stack 的大小来判断是否存在回路。需要注意的是在记录时一定要等深度优先回来之后再入栈,如下图中的 4 节点是要等遍历完 5 和 6 回来之后再把 4 入栈。这样可以理解为我们先剔除了4->5->6->4 这个回路,然后再去剔除新的回路,否则就会发生错误。
int matrix[MAX_SIZE][MAX_SIZE];
void euler(int i, int n, int *stack, int *pc) {
for (int j = 0; j < n; j++) {
if (matrix[i][j] != 0) {
matrix[i][j] = 0; // 每条路只能走一遍
matrix[j][i] = 0;
euler(j, n, stack, pc);
stack[(*pc)++] = j; // 这里一定是在深度优先完了之后再入栈
}
}
}
int main()
{
int n, m, u, v;
int stack[MAX_SIZE] = {0};
int pc = 0;
scanf("%d%d", &n, &m);
memset(matrix, 0, sizeof(matrix));
for (int i = 0; i < m; i++) {
scanf("%d%d", &u, &v);
matrix[u - 1][v - 1] = 1;
matrix[v - 1][u - 1] = 1; // 无向图的连接方式
}
euler(0, n, stack, &pc);
stack[pc++] = 0;
for (int i = pc - 1; i >= 0; i--) {
printf("%d ", stack[i] + 1);
}
printf("\n");
return 0;
}
Last modified on 2022-12-30
