算法介绍 #
并查集主要用于集合之间的操作。对于两个集合而言,它们一般能做的就是将两个集合的元素合并(并)。同时,我们往往会希望知道两个元素在不在同一个集合中(查)。由此便引出了并查集这种数据结构。
为了便于理解,我们先将问题进行简化。假如目前摆在我们面前的有这样一个图
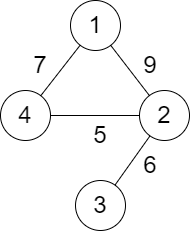
在这个图中 每两个节点之间的连通关系和它们之间的距离可以用如下的二维数组来表示,
[[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
我们现在希望找到一种数据结构,从我们给定的联通关系中从 0 构建上面的那张图,并且可以高效地实现查找某一个节点在不在这张连通图里面。所以我们可以将它们用一个一维数组的方式来存储,如下图所示
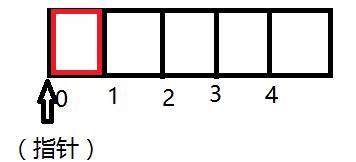
我们将数组的下标用来表示元素节点,用数组下标对应的值来表示它们的父亲节点,这样就可以构建一个father数组。我们在初始化的时候可以将它们的父亲节点都初始化成自己,这时对应的图就是每个节点各自都不连通,然后我们在用并查集的并来对这个数组进行赋值(这时我们不妨先假设father数组已经构建好了)。
public int findFather(int n) {
if (fa[n] == n) {
return n;
}
return findFather(fa[n]);
}
public void unionSet(int i, int j) {
int faI = findFather(i);
int faJ = findFather(j);
if (faI != faJ) {
fa[faJ] = faI;
}
}
我们首先来观察 findFather 这个函数,这个函数做的事情就是找一个节点的根节点。如果一个节点的父结点就是它自己的话说明我们已经找到这棵树的根了,然后就返回这个节点的 id。否则,我们就找这个节点父结点的父结点,也就是它的“爷爷节点”,逐层向上递归,最终我们一定能找到这个节点所在集合的根节点,并且保证时间复杂度是线性的。
然后我们再来观察 unionSet 这个函数,这个函数首先会去找两个元素i,j 的根节点,如果它们的根节点是一样的,说明它们在一个集合里,这里我们不进行操作;否则,说明它们在不同的集合,这时我们要做的操作就是把这两个集合合并起来,我们只需要让其中一个根节点的父结点变成另一个节点就可以了。这样我们就完成了两个集合的合并操作。
到这里并查集的任务基本已经完成了,我们来思考一下有没有什么可以进一步优化的空间。手下来看 findFather 这个函数,我们显然可以知道它的时间复杂度是线性的。也就是说,如果我们的运气足够差,当我们目前构建的这个树退化成了单向链表,在时间上我们就要付出更大的成本了。所以可以考虑有一种优化的方式,因为我们在调用这个函数的时候只想知道根节点是谁,并不一定要记录每个节点的父结点,所以我们可以在初始化的时候将每个节点的父结点都设置为根节点,代码表示如下
public int findFather(int n) {
if (fa[n] == n) {
return n;
}
return fa[n] = findFather(fa[n]);
}
这段代码需要说明的一点是 fa[n] = findFather(fa[n]) 这个表达式本身是有返回值的,返回值是 fa[n] 最终被赋予的那个值。
然后我们再来考虑优化 unionSet 函数,这个函数在合并两个集合的时候是随机将一个节点的变成另一个节点的父结点,这种操作有可能会使合并后的树的高度增加。一种优化的办法就是将高度比较低的那棵树的根节点的父结点变成高度比较高的那棵树的根节点,这样树的高度就保证在高度较高的那颗树的高度了。下面我们给出优化的代码
public void unionSet(int i, int j) {
int faI = findFather(i);
int faJ = findFather(j);
if (faI == faJ) {
return;
}
if (rank[faI] > rank[faJ]) {
fa[faJ] = faI;
} else {
fa[faI] = faJ;
if (rank[faI] == fa[faJ]) {
rank[faJ]++;
}
}
}
这段代码中我们引入了一个 rank 数组用来表示以 i 为根节点的树的高度,它应该和 fa 数组同时被初始化,并且初始化的值均为 1.
实战演练 #
下面我们来看一道 leetcode 的题目来真正感受一下并查集的应用,题目的详细信息可以点击这里 . 我们这里直接给出题解参考代码来对代码进行解释
class Solution {
int[] fa;
int[] val; // 表示以节点 i 为根节点的集合中距离最小的边
public int findFather(int n) {
if (fa[n] == n) {
return n;
}
return fa[n] = findFather(fa[n]);
}
public void unionSet(int i, int j, int distance) {
int faI = findFather(i);
int faJ = findFather(j);
if (faI > faJ) { // 这里我们确保根是编号最小的节点
int tmp = faI;
faI = faJ;
faJ = tmp;
}
fa[faJ] = faI;
val[faI] = Math.min(Math.min(val[faI], val[faJ]), distance);
}
public int minScore(int n, int[][] roads) {
fa = new int[n];
val = new int[n];
for (int i = 0; i < n; i++) {
fa[i] = i;
val[i] = (int)1e5; // 将节点间距离初始化为一个无穷大的数
}
for (int i = 0; i < roads.length; i++) {
merge(roads[i][0] - 1, roads[i][1] - 1, roads[i][2]);
}
return val[0];
}
}
这道题能用这种方法的一个前提条件是题目中说明了 测试数据保证城市 1 和城市n 之间 至少 有一条路径。也就是说这些节点最终能够构成一个连通图,在这个条件下我们这段代码才能成立。
上面的题目主要针对的场景比较简单,因为数组的下标刚好可以用来表示节点,同时集合的合并页很容易理解。下面这道题是并查集的一个进阶的题目,“矩阵查询可获得的最大分数”,详细信息可以点击这里 ,同样我们只给出参考的题解。
class Pair {
int x;
int y;
public Pair(int x, int y) {
this.x = x;
this.y = y;
}
}
class Solution {
Pair[][] fa;
int[][] size;
Pair[] sortGrid;
Integer[] sortQueries;
public Pair findFather(Pair pair) {
if (fa[pair.x][pair.y] == pair) {
return pair;
}
return fa[pair.x][pair.y] = findFather(fa[pair.x][pair.y]);
}
public void unionSet(Pair pairX, Pair pairY, int[][] grid, int num, int m, int n) {
if (pairY.x < 0 || pairY.x >= m || pairY.y < 0 || pairY.y >= n) {
return;
}
Pair faX = findFather(pairX);
Pair faY = findFather(pairY);
if (faX == faY) {
return;
}
if (grid[pairY.x][pairY.y] >= num) {
return;
}
fa[faX.x][faX.y] = faY;
size[faY.x][faY.y] += size[faX.x][faX.y];
}
public int[] maxPoints(int[][] grid, int[] queries) {
int k = queries.length;
int m = grid.length;
int n = grid[0].length;
int[] res = new int[k];
fa = new Pair[m][n];
size = new int[m][n];
sortGrid = new Pair[m * n];
sortQueries = new Integer[k];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
fa[i][j] = new Pair(i, j);
size[i][j] = 1;
}
}
for (int i = 0; i < k; i++) {
sortQueries[i] = i;
}
Arrays.sort(sortQueries, new Comparator<Integer>() {
@Override
public int compare(Integer a, Integer b) {
return queries[(int)a] - queries[(int)b];
}
});
int cnt = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sortGrid[cnt++] = new Pair(i, j);
}
}
Arrays.sort(sortGrid, new Comparator<Pair>() {
@Override
public int compare(Pair a, Pair b) {
return grid[a.x][a.y] - grid[b.x][b.y];
}
});
boolean[][] isVisited = new boolean[m][n];
int j = 0;
for (int i = 0; i < k; i++) {
int idx = sortQueries[i];
while (j < cnt && queries[idx] > grid[sortGrid[j].x][sortGrid[j].y]) {
unionSet(sortGrid[j], new Pair(sortGrid[j].x + 1, sortGrid[j].y), grid, queries[idx], m, n);
unionSet(sortGrid[j], new Pair(sortGrid[j].x - 1, sortGrid[j].y), grid, queries[idx], m, n);
unionSet(sortGrid[j], new Pair(sortGrid[j].x, sortGrid[j].y + 1), grid, queries[idx], m, n);
unionSet(sortGrid[j], new Pair(sortGrid[j].x, sortGrid[j].y - 1), grid, queries[idx], m, n);
j++;
}
if (queries[idx] <= grid[0][0]) {
continue;
}
Pair tmp = new Pair(0, 0);
Pair fatherOfTmp = findFather(tmp);
res[idx] = size[fatherOfTmp.x][fatherOfTmp.y];
}
return res;
}
}
Last modified on 2022-12-10