KMP Algorithm | KMP算法

/ 2021-07-23 / 300 Words/has been Read Times

背景 #

KMP算法是用来解决字符串的匹配问题的。对于字符串匹配问题，我们首先想到的就是暴力破解法。

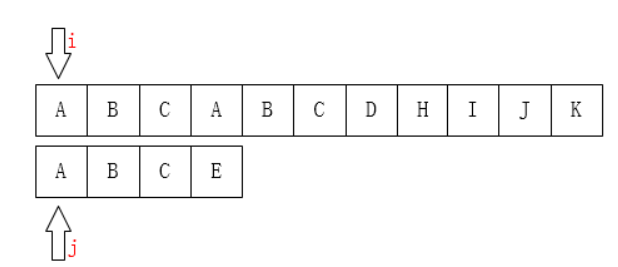
用指针i,j来说明，第一个位置下标以0开始。如果匹配则继续比较下一位。否则将j的值清0，i的值也要回到最开始匹配成功的位置重新开始比较，如下图。

public int strStr(String haystack, String needle) {
    if (needle == "") {
        return 0;
    }

    for (int i = 0; i < haystack.length() - needle.length() + 1; i++) {
        for (int j = 0; j < needle.length(); j++) {
            if (needle.charAt(j) != haystack.charAt(j + i)) {
                break;
            }
            if (j == needle.length() - 1) {
                return i;
            }
        }
    }
    return -1;
}

暴力算法有一个很严重的问题就是一旦不匹配就要从目标字符串的第一个字符开始从头计算。如果是人为来寻找的话，我们肯定不会这样做，因为主串匹配失败的位置(i=3)前面除了第一个A之外再也没有A了，我们为什么能知道主串前面只有一个A？因为我们已经知道前面三个字符都是匹配的[1] 。换句话说是我们知道匹配失败位置之前的元素都不是A，所以我们可以直接将i指针移动到下图所示的位置：

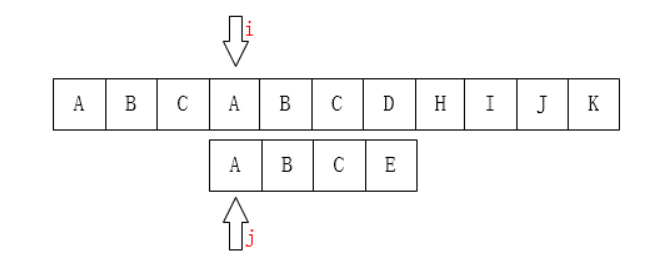
这样就避免了回退的问题，其实前面的例子中要匹配的字符串（ABCE）中并没有出现相同的字符，所以多少会有一点巧合的意思。现在我们用另外一个例子来说明。假设文档的字符串source = “abaabaabca”, 目标字符串target = “abaabca”

匹配到高亮显示的位置就需要重新调整j的值，这时自然不能像最开始的例子那样直接跳到不匹配的位置,这样最终会返回匹配失败。其实应该跳到的位置如下图所示：

但其实按照上面所描述的这样，如果不匹配，其实原字符串的指针和目标字符串的指针也都向后回退了，虽然回退的步数有所减少。我们能不能想到一个办法让指针不发生回退呢，即直接从匹配失败的位置处继续往下扫描，如下图所示：

从上面的图可以看出指针i依然停留在原来的位置，指针j则跳回了它对应的位置。这次移动是非常理想的，同时要完成这个效果，我们也必须考虑到一个条件，就是要求k之前的字符都要和原字符串中的字符是匹配的，并且匹配的个数应该最多。

我们可以通过下图来比较前后两种不同的差异：

字符串的前缀和后缀 #

那现在的问题就是我们该怎么知道满足上面两种条件的字符是哪个呢，就是说怎么确保让指针j跳到合适的位置呢？我们先把目前已知的条件列出来：

目前遍历的target字符串是"abaabc"，后面的我们不清楚是什么，所以没法考虑后面的情况；
已知最后一个字符’c’是不匹配的；
‘c’以前的字符都是匹配的。

结合目前的条件，我们可以初步有一个大胆的设想，“abaab"的前2个字符是"ab”，我们发现后面也出现了"ab"。会不会是因为前后有相同的序列，并且它们都是已知和原字符串匹配，所以我们才把j指针的位置放在"ab"后面的呢？在解释这个问题之前我们先来了解一个字符串的前缀和后缀的概念：

前缀集合就是不包括最后一个字符，从头往后遍历的子字符串的集合；同样的后缀集合是不包括第一个字符，从后往前遍历的子字符串的集合。

例如：字符串：“hello”

前缀集合: [ h, he,hel, hell]
后缀集合：[ o,lo,llo,ello ]
集合的共有元素的长度为0.

同样，“A”的前缀和后缀都为空集，共有元素的长度为0. target = “abaabca"的前后缀集合具体可参考下表：

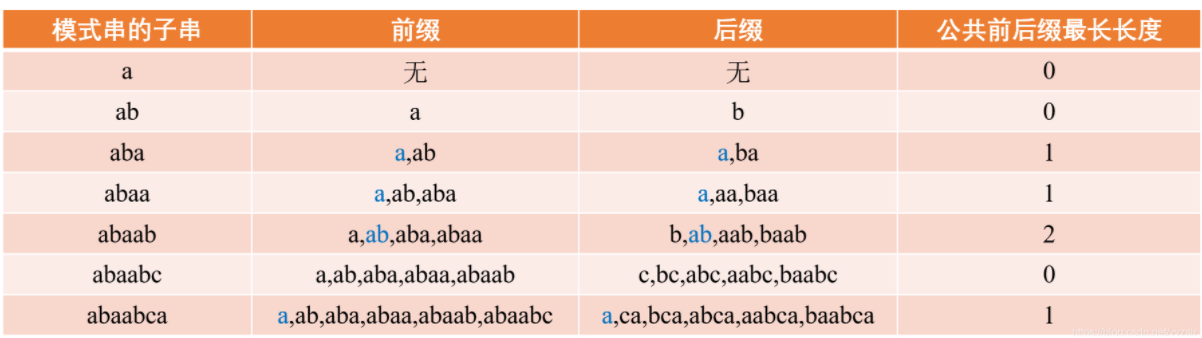
这样，公共前后缀最长长度就会和串P的每个字符产生一种对应关系.

这个表最后一列的含义是当前子串所拥有的公共前后缀最长长度。例如"abaabc"并没有公共前后缀。

那我们现在回到之前第一次匹配失败的位置，就是因为’a’和’c’不匹配，我们先把匹配失败的字符’c’去掉，target之前的子串就是"abaab”，这个串的最大公共前后缀长度为2，也就是说这个字符串最前面的两个字符和最后面的两个字符是一样的。

我们在’c’处虽然匹配失败了，但是我们可以肯定在之前都是匹配成功的。这也就是说最开始的两个字符和最后的两个字符都能匹配，而恰好它们又都相同，那我们直接把j指针移到第三个元素那里，让i和它进行匹配不就行了，反正我们知道前两个是成功匹配的。

但是虽然理论上这个可行了，实际上我们怎么操作呢，最主要的就是这个最大公共前后缀怎么计算和存储的问题。只要知道了这个，我们一旦出现不匹配，就把指针j赋值为最大公共前后缀的数就可以了。

next数组 #

于是就出现了一个和要匹配的字符串“abaabce”对应的数组next来指明这样的信息。Next里面存的值称为部分匹配值，部分匹配值就是前缀和后缀的最长的共有元素的长度

next数组的具体的值计算如下。

首先我们可以肯定假字符串的长度为1，那最大公共子串长就是0
否则，我们就假设任意一个子串k(0<k<target.length), 它的最大公共子串长为：

$maxLength(i) = \left\{ \begin{array}{**lr**} maxLength(j - 1) , while(dest[i] != dest[j] and j > 0 )& \\ j++ , other& \end{array} \right.$

这里的i指向后缀末尾，所以i只能从1开始；j指向前缀末尾，同时j还代表了最大公共前后缀的长度。

这里是比较两个序列，它们的顺序是相同的，要和回文数区别开来。

这个公式的大致意思是说，只要前后缀末尾的字符不相等，那就把前缀的下标值-1，然后继续匹配，直到对应的值相等。同样这里要保证j>0, 因为0是初始位置，到初始位置就不能再回退了；相等的话就表示成功匹配，将最大公共字符串长度+1，也即让前后缀下标+1继续匹配下一个（只不过后缀下标+1是在循环体里实现的）。

代码实现如下：

public int[] kmpNext(String dest) {
    int[] next = new int[dest.length()];
    next[0] = 0; //如果字符串是长度为1 部分匹配值就是0
    for (int i = 1, j = 0; i < dest.length(); i++) {      
        while (j > 0 && dest.charAt(i) != dest.charAt(j)) {
            j = next[j - 1];
        }
        if (dest.charAt(i) == dest.charAt(j)) {
            j++;
        }
        next[i] = j; 
    }
    return next;
}

上面的循环中如果i表示字符串的长度，从长度为1的字符串对应的最长公共前后缀开始，直到字符串的长度是dest.length()。对于长度为k的字符串来说，在dest.charAt(k) != dest.charAt(j)的情况下，它的最长公共前后缀就是当前已知的j-1对应的值。否则就是j++。因为前缀必须是从下标0处开始的，所以只用j就能知道结果。到这一步我们就已经得到了next数组所对应的值，可以进行下一步的操作了。

下一步就是要实现整个KMP算法了，我们继续完成前面的问题：

source = “abaabaabca”,target = “abaabca”

代码如下：

public int strStr(String haystack, String needle) {
    if (needle == "") {
        return 0;
    }
    int[] next = kmpNext(needle);
    for (int i = 0, j = 0; i < haystack.length(); i++) {
        while (j > 0 && needle.charAt(j) != haystack.charAt(i)) {
            j = next[j - 1];
        } 
        if (needle.charAt(j) == haystack.charAt(i)) {
            j++;
        } 
        if (j == needle.length()) {
            return i - j + 1;
        }
    }
    return -1;
}

比较暴力匹配算法我们可以看到，基本只有当匹配失败之后j指针的变化需要根据next指针进行修改。

到这里KMP算法基本就完成了，还有一种解释方法是用有限状态自动机来解释，如果想更深入地了解KMP算法，可以参考这篇博客[2] 或者是人民邮电出版社出版的算法（第四版）第5章的部分，这些都涉及到了有限状态自动机的部分。

参考 #

^ https://www.cnblogs.com/dusf/p/kmp.html
^ https://www.cnblogs.com/zzuuoo666/p/9028287.html

Last modified on 2021-07-23