目前网络上和教材种对这两种排序算法大多是采用递归的方式来实现的,但是非递归的方式较少。另外这两种排序算法也各有特点,像是一对孪生兄弟。首先快排是先排序后分块,归并是先分块后排序,这点在递归方式实现中体现地尤为明显;同时快排是不稳定的排序,归并是稳定的排序;快排不需要额外的内存空间,而归并需要一个和输入数组相同的内存空间。
快速排序的非递归实现 #
如上所述,快排是要先把一个元素排到对应的位置然后再分块,这个很容易用栈来实现,同时在遇到将递归转为非递归的问题的时候,我们可以首先思考用栈能否实现。具体代码如下:
public static int[] QuickSort(int[] arr, int left, int right) {
Stack<Integer> stack = new Stack<>();
if (left < right) {
stack.push(left);
stack.push(right);
while (!stack.isEmpty()) {
int height = stack.pop();
int low = stack.pop();
int index = partition(arr, low, height);
if (index - 1 > low) {
stack.push(low);
stack.push(index - 1);
}
if (index + 1 < height) {
stack.push(index + 1);
stack.push(height);
}
}
}
return arr;
}
private static int partition(int[] list, int first, int last) {
int pivot = list[first];
int low = first + 1;
int high = last;
while (high > low) {
while (low <= high && list[low] <= pivot)
low++;
while (low <= high && list[high] > pivot)
high--;
if (high > low) {
int temp = list[high];
list[high] = list[low];
list[low] = temp;
}
}
while (high > first && list[high] >= pivot)
high--;
if (pivot > list[high]) {
list[first] = list[high];
list[high] = pivot;
return high;
} else {
return first;
}
}
归并排序的非递归实现 #
归并不同于快排,它要求首先把整个数组分成最小的块,每个块是有序的,然后再逐层往上排序。这样就使得没法用栈来实现。具体的代码如下:
public static void mergeSort(int[] arr, int[] temp) {
// 从 1开始分割,与递归不同的是,递归由数组长度一分为二最后到1,
// 而非递归则是从1开始扩大二倍直到数组长度
int len = 1;
while (arr.length > len) {
// 完全二叉树一层内的遍历
for (int i = 0; i + len <= arr.length - 1; i += len * 2) {
int left = i;
int mid = i + len - 1;
int right = i + len * 2 - 1;
// 防止超出数组长度
if (right > arr.length - 1)
right = arr.length - 1;
// 合并排序相同
merge(arr, left, mid, right, temp);
}
// 下一层
len *= 2;
}
}
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left;
int j = mid + 1;
int t = 0;
while (i <= mid && j <= right) {
if(arr[i] <= arr[j]) {
temp[t] = arr[i];
t += 1;
i += 1;
} else {
temp[t] = arr[j];
t += 1;
j += 1;
}
}
while( i <= mid) {
temp[t] = arr[i];
t += 1;
i += 1;
}
while( j <= right) {
temp[t] = arr[j];
t += 1;
j += 1;
}
t = 0;
int tempLeft = left;
while(tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
比较几种不同方式实现的时间复杂度 #
快排和归并的时间复杂度都是nlog(n), 本文用python对几种方式的实现作图进行比较,观察不同方式的时间复杂度,如下图:
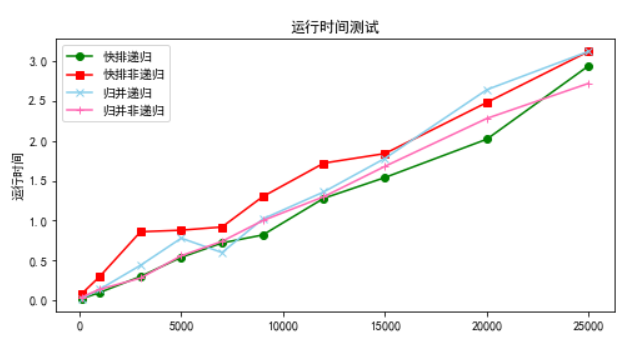
可以看到基本都满足nlog(n)的时间复杂度。
Last modified on 2021-05-07